探索遗传算法的应用-题库智能组卷
前言
在我做一个教学系统的项目时,遇到了一个问题场景,需要实现一个题库的功能,存放许多携带不同参数的题目,并且可以按照教师的参数需求,进行智能随机组卷。
一开始我以为是个比较简单的问题,准备自己手写个简单算法,能实现效果就行,但随着题目和题库的大致模型构思完,题目的参数变多,需要考虑的问题、意外的情况太多,自己写的代码屡屡出现问题,最终决定选择一套系统的、成体系的算法来重构这部分代码。
上网查阅了相关资料,找到了两种算法:1.回溯算法 2.遗传算法
在对比了两种算法的优劣之后,我选择了遗传算法,因为它更为可控,算法具有更好的收敛性,效率更高,并且相对来说消耗内存更少。
遗传算法简介
算法的一些概念
概念1:基因和染色体
在遗传算法中,我们首先需要将要解决的问题映射成一个数学问题,也就是所谓的“数学建模”,那么这个问题的一个可行解即被称为一条“染色体”。一个可行解一般由多个元素构成,那么这每一个元素就被称为染色体上的一个“基因”。
比如说,对于如下函数而言,[1,2,3]、[1,3,2]、[3,2,1]均是这个函数的可行解(代进去成立即为可行解),那么这些可行解在遗传算法中均被称为染色体。
这些可行解一共有三个元素构成,那么在遗传算法中,每个元素就被称为组成染色体的一个基因。
概念2:适应度函数
在自然界中,似乎存在着一个上帝,它能够选择出每一代中比较优良的个体,而淘汰一些环境适应度较差的个人。那么在遗传算法中,如何衡量染色体的优劣呢?这就是由适应度函数完成的。适应度函数在遗传算法中扮演者这个“上帝”的角色。
遗传算法在运行的过程中会进行N次迭代,每次迭代都会生成若干条染色体。适应度函数会给本次迭代中生成的所有染色体打个分,来评判这些染色体的适应度,然后将适应度较低的染色体淘汰掉,只保留适应度较高的染色体,从而经过若干次迭代后染色体的质量将越来越优良。
概念3:交叉
遗传算法每一次迭代都会生成N条染色体,在遗传算法中,这每一次迭代就被称为一次“进化”。那么,每次进化新生成的染色体是如何而来的呢?——答案就是“交叉”,你可以把它理解为交配。
交叉的过程需要从上一代的染色体中寻找两条染色体,一条是爸爸,一条是妈妈。然后将这两条染色体的某一个位置切断,并拼接在一起,从而生成一条新的染色体。这条新染色体上即包含了一定数量的爸爸的基因,也包含了一定数量的妈妈的基因。
在每完成一次进化后,都要计算每一条染色体的适应度,然后采用如下公式计算每一条染色体的适应度概率。那么在进行交叉过程时,就需要根据这个概率来选择父母染色体。适应度比较大的染色体被选中的概率就越高。这也就是为什么遗传算法能保留优良基因的原因。
概念4:变异
交叉能保证每次进化留下优良的基因,但它仅仅是对原有的结果集进行选择,基因还是那么几个,只不过交换了他们的组合顺序。这只能保证经过N次进化后,计算结果更接近于局部最优解,而永远没办法达到全局最优解,为了解决这一个问题,我们需要引入变异。
变异很好理解。当我们通过交叉生成了一条新的染色体后,需要在新染色体上随机选择若干个基因,然后随机修改基因的值,从而给现有的染色体引入了新的基因,突破了当前搜索的限制,更有利于算法寻找到全局最优解。
概念5:复制
每次进化中,为了保留上一代优良的染色体,需要将上一代中适应度最高的几条染色体直接原封不动地复制给下一代。
假设每次进化都需生成N条染色体,那么每次进化中,通过交叉方式需要生成N-M条染色体,剩余的M条染色体通过复制上一代适应度最高的M条染色体而来。
遗传算法的流程
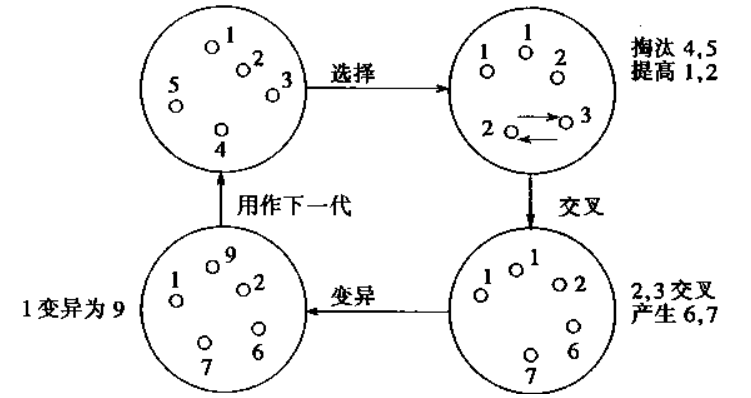
在算法初始阶段,它会随机生成一组可行解,也就是第一代染色体。然后采用适应度函数分别计算每一条染色体的适应程度,并根据适应程度计算每一条染色体在下一次进化中被选中的概率。
通过“交叉”,生成N-M条染色体;再对交叉后生成的N-M条染色体进行“变异”操作;然后使用“复制”的方式生成M条染色体;
N条染色体生成完毕,紧接着分别计算N条染色体的适应度和下次被选中的概率。至此,一轮进化就完成了。
遗传算法对组卷问题的实现
求解目标
根据教师输入的试卷参数要求,用遗传算法从题库中抽取题目生成个体和种群,多次迭代进化最终达到预定期望。并探索总结出不同类型、个数的参数,即不同的个体基因编码种类对于最终求解的影响,以及研究种群在不同的进化参数下,对于迭代过程和结果的影响。
限制条件
- 教师输入的参数,例如题目数量,题目类型,题型分值,难度系数,章节。
- 题库内题目的数量,种类,难度
输入样例
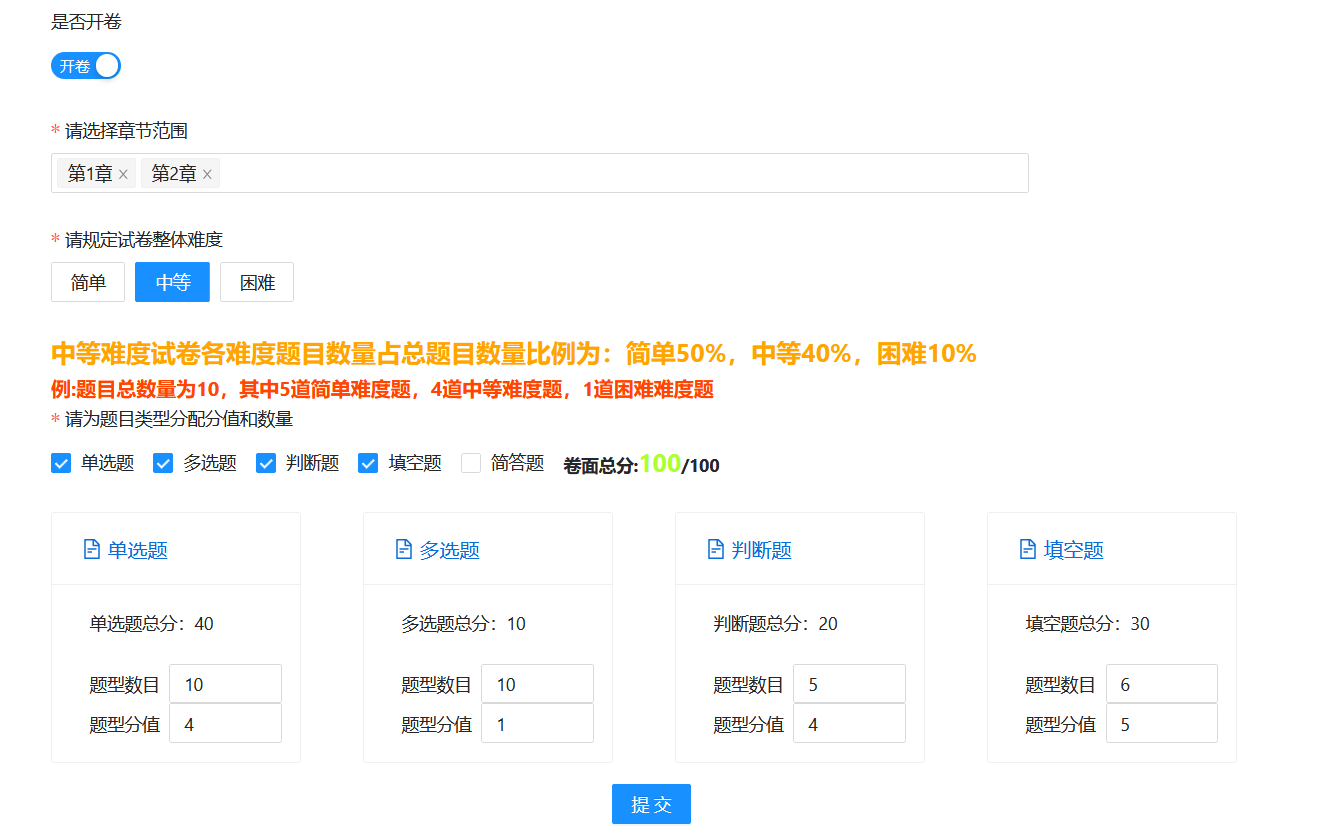
前端向后端传递输入参数,整合完最终的数据对象
1 | /** |
算法实现步骤
创建实体类和对应模型关系
- 题目:成员变量 —> 题目id、难度、题型
- 试卷个体:成员变量 —> 试卷id,题目list、个体适应度、个体难度系数
- 试卷种群:成员变量 —> 试卷list
- 遗传算法实现Service:成员变量 —> 变异概率、锦标赛选择方法规模比例
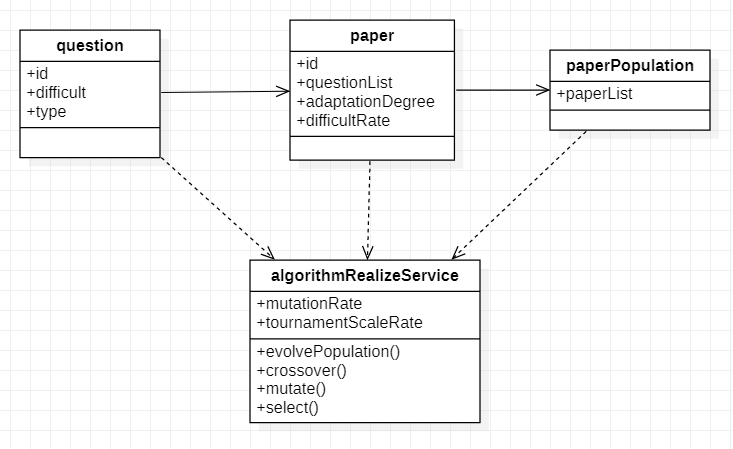
具体实现原理
结合具体问题实现遗传算法,一开始我将试卷个体的难度系数以及不同的题目作为整数基因编码。题目的难度分为0,1,2三种难度,分别对应简单,中等,困难。
试卷个体难度系数公式: (D-难度系数,d-题目难度,s-题目分值)
种群在初始化阶段会从数据库中随机抽取符合教师输入的规则r的对应若干个题目分别随机放入n个试卷个体内(n为种群规模),这一过程要避免一张试卷中出现重复题目。从而算出每个个体的适应度。
试卷个体适应度公式:(ED为期望难度系数)
初始化构建完毕的种群,其中的个体应该满足总分
具体实现步骤
PS:只有实现过程的部分代码,可以阅读交流学习,光靠这部分代码无法完整运行整个流程。
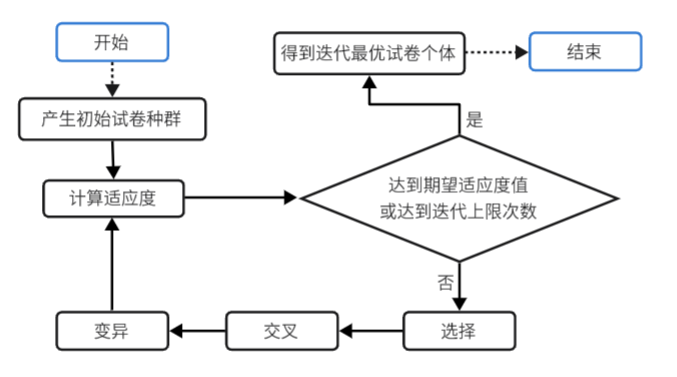
-
初始化。设置进化代数计数器,设置n作为种群规模,将抽取题库用到的Dao层控制器导入种群作为初始化工具,设置最大进化代数(避免死循环),如果算法要达到全局最优解可能要经过很多次的进化,这极大影响系统的性能。那么我们就可以在算法的精确度和系统效率之间寻找一个平衡点。我们可以事先设定一个可以接收的结果范围,当算法进行x次进化后,一旦发现了当前的结果已经在误差范围之内了,那么就终止算法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40/**
* 算法迭代入口函数
*/
public Result getExaminationPaper(String userId,examinationPaperMakeConfig rule) {
ExaminationPaper resultPaper = null;
int loop = 25;
// 适应度期望值 0-1 的数 满分是1
double expand = 0.95;
ExaminationPopulation population;
// 初始化种群
for (int i = 0; i < loop; i++) {
// 迭代计数器
int count = 0;
int runCount = 6;
population = new ExaminationPopulation(25, rule ,tExaminationQuestionDao,examinationDao );
if (population.getErrorMsg()!=null){
System.out.println("种群初始化失败,"+population.getErrorMsg());
return Result.error("018",population.getErrorMsg());
}
System.out.println("种群初始化完成,执行遗传算法进行迭代====================================");
System.out.println("种群初始最优个体适应度:"+population.getMostFitOne().getAdaptationDegree());
while (count < runCount && population.getMostFitOne().getAdaptationDegree() < expand) {
count++;
population = examinationAlgorithmRealizeService.evolvePopulation(population, rule);
System.out.println("第 " + count + " 次进化,最优个体适应度为:" + population.getMostFitOne().getAdaptationDegree());
}
System.out.println("共进化: " + count +" 次");
System.out.println("最终迭代得出最优个体适应度为: "+population.getMostFitOne().getAdaptationDegree());
System.out.println("期望适应度为"+expand+"(分值0-1分): "+population.getMostFitOne().getAdaptationDegree());
resultPaper = population.getMostFitOne();
if (resultPaper.getAdaptationDegree() > expand){
break;
}
}
ExaminationPaperResultQuestionId resultQuestionIds = resultPaper.getAllQuestionIds();
resultQuestionIds.setRule(rule);
Map resMap = Map.of("questionIdList",resultQuestionIds.getQuestionIdList(),"questionScore",resultQuestionIds.getRule().getQuestionScore());
return Result.success(resMap,"组卷成功,与期望难度匹配度为: "+String.format("%.1f",resultPaper.getAdaptationDegree()*100)+"%");
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102/**
* 试卷种群
* 题型对应数字:单选0,多选1,判断2,填空3,简答4
* (包含多套试卷)
*/
public class ExaminationPopulation {
//试卷数组
private ExaminationPaper[] papers;
//自动组卷规则
examinationPaperMakeConfig rule;
/**
* 初始化一种题型
* (从数据库中获取题目)
*/
private void initializeQuestion(int type, String errorMsg, ExaminationPaper paper) {
//mybatis筛选器
QueryWrapper<TExaminationQuestion> wrapper = new QueryWrapper();
wrapper.lambda().eq(TExaminationQuestion::getType,type);
.eq(TExaminationQuestion::getIsApproved,1);
.in(TExaminationQuestion::getChapter,rule.getChapterRange());
//题目数组
List<TExaminationQuestion> questionList = tExaminationQuestionDao.selectList(wrapper);
if (questionList.size() < rule.getQuestionCounts()[type]) {
this.initializeErrorMsg = errorMsg;
return;
}
ArrayList<Integer> questionNums = new ArrayList();
for (int i = 0; i < questionList.size(); i++) {
questionNums.add(i);
}
Random random = new Random();
for (int j = 0; j < rule.getQuestionCounts()[type]; j++) {
int index = random.nextInt(questionNums.size());
//试卷随机添加题目
paper.addQuestion(type,questionList.get(questionNums.get(index)));
//移除该数组下表的题目,避免添加重复题目
questionNums.remove(index);
}
}
/**
* 初始化种群
* @param populationSize 种群规模
* @param rule 规则
*/
public ExaminationPopulation(int populationSize, examinationPaperMakeConfig rule,tExaminationQuestionDao questionDao,ExaminationDao eDao) {
// Dao层控制器
this.examinationDao = eDao;
this.tExaminationQuestionDao = questionDao;
this.rule = rule;
papers = new ExaminationPaper[populationSize];
ExaminationPaper paper;
for (int i = 0; i < populationSize; i++) {
//创建一个新试卷个体
paper = new ExaminationPaper(i,rule.getTotalMark(),rule);
// 单选题
if (rule.getQuestionCounts()[0] > 0 && initializeErrorMsg == null) {
initializeQuestion(0,"单选题数量不够", paper);
}
// 多选题
if (rule.getQuestionCounts()[1] > 0 && initializeErrorMsg == null) {
initializeQuestion(1,"多选题数量不够", paper);
}
// 判断题
if (rule.getQuestionCounts()[2] > 0 && initializeErrorMsg == null) {
initializeQuestion(2,"判断题数量不够", paper);
}
// 填空题
if (rule.getQuestionCounts()[3] > 0 && initializeErrorMsg == null) {
initializeQuestion(3,"填空题数量不够", paper);
}
// 简答题
if (rule.getQuestionCounts()[4] > 0 && initializeErrorMsg == null) {
initializeQuestion(4,"简答题题数量不够", paper);
}
// 计算试卷适应度
paper.setAdaptationDegree();
papers[i] = paper;
if (initializeErrorMsg != null){
break;
}
}
}
/**
* 获取种群中最优秀个体
*/
public ExaminationPaper getMostFitOne() {
ExaminationPaper paper = papers[0];
for (int i = 1; i < papers.length; i++) {
if (paper.getAdaptationDegree() < papers[i].getAdaptationDegree()) {
paper = papers[i];
}
}
return paper;
}
} -
计算适应度。 先根据每张试卷所有题目的难度、分值等参数计算出个体的难度系数,再根据难度系数计算初始种群中每个体的适应度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39/**
* 计算试卷个体难度系数
* 计算公式: (难度*分数)/总分
* @return 难度系数
*/
public double getDifficultyRate() {
if (difficulty == 0.0){
double stepDifficulty = 0.0;
for (int i = 0; i < questionList.length; i++) {
for (t_examination_question question : questionList[i]) {
stepDifficulty += rule.getQuestionScore()[i] * question.getDifficulty();
}
}
stepDifficulty = stepDifficulty / (totalScore*2);
this.difficulty = stepDifficulty;
return stepDifficulty;
}else
return difficulty;
}
/**
* 计算个体适应度
* ED为期望难度系数,D为种群个体难度系数
*/
public void setAdaptationDegree() {
double step = 0;
switch (rule.getDifficulty()){
case 0:
step = 0.2;
break;
case 1:
step = 0.3;
break;
case 2:
step = 0.4;
break;
}
adaptationDegree = 1 - Math.abs(step - getDifficultyRate());
} -
选择。选择是用来确定重组或交叉的个体,以及被选个体将产生多少子个体。按照上面得出的个体适应度进行父代个体的选择。可以挑选以下算法:轮盘赌选择、随机遍历抽样、局部选择、截断选择、锦标赛选择。我在此选择的是锦标赛选择方法,需要设置锦标赛选择规模系数j。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27/**
* 获取指定规模下随机的种群中最优秀个体
* (用于锦标赛选择方法)
* 如果规模大小 > 种群数量大小,或小于0,则会返回null
* @param scale 规模大小int
*/
public ExaminationPaper getMostFitOne(int scale) {
ExaminationPaper paper = null;
if (scale > 0 && scale <= papers.length){
ArrayList<Integer> selectPaperId = new ArrayList();
for (int i = 0; i < papers.length; i++) {
selectPaperId.add(i);
}
Random random = new Random();
for (int i = 0; i < papers.length - scale; i++) {
int step = random.nextInt(selectPaperId.size());
selectPaperId.remove(step);
}
paper = papers[selectPaperId.get(0)];
for (int i = 1; i < selectPaperId.size(); i++) {
if (paper.getAdaptationDegree() < papers[selectPaperId.get(i)].getAdaptationDegree()) {
paper = papers[selectPaperId.get(i)];
}
}
}
return paper;
} -
交叉。基因重组是结合来自父代交配种群中的信息产生新的个体。依据个体编码表示方法的不同,可以有以下的算法:实值重组;离散重组;中间重组;线性重组;扩展线性重组。二进制交叉、单点交叉、多点交叉、均匀交叉、洗牌交叉、缩小代理交叉。我在实现过程中选择的是洗牌交叉,从一个父个体中取一半的基因,即一半的题目,再从另一个父个体中取一半,随机打乱后就生成了新的子个体基因。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62/**
* 交叉产生下一代函数
* @param parent1
* @param parent2
* @return
*/
public ExaminationPaper crossover(ExaminationPaper parent1, ExaminationPaper parent2, examinationPaperMakeConfig rule) {
// 创建child paper
ExaminationPaper child = new ExaminationPaper(0,rule.getTotalMark(),rule);
List<TExaminationQuestion>[] questionList = new List[5];
for (int i = 0; i < questionList.length; i++) {
questionList[i] = new ArrayList<>();
}
// 储存交叉生成的子试卷中题目id,避免重复
List<TExaminationQuestion>[] parent1QuestionList = new List[5];
List<TExaminationQuestion>[] parent2QuestionList = new List[5];
for (int i = 0; i < 5; i++) {
parent1QuestionList[i] = new ArrayList<>(parent1.getQuestionList()[i]);
parent2QuestionList[i] = new ArrayList<>(parent2.getQuestionList()[i]);
}
List<Integer> existQuestionId = new ArrayList<>();
Random random = new Random();
for (int i = 0; i < 5; i++) {
boolean run = true;
// 子试卷题目数组一种题型目标大小
int targetSize = parent1QuestionList[i].size();
int runningTimes = 0;
while (run){
//若满足条件则从父类1一中随机抽取一道不重复的题目添加
if (parent1QuestionList[i]!=null){
if (parent1QuestionList[i].size() > 0 && questionList[i].size()<targetSize){
int step = random.nextInt(parent1QuestionList[i].size());
if (!existQuestionId.contains(parent1QuestionList[i].get(step).getQuestionId())){
questionList[i].add(parent1QuestionList[i].get(step));
existQuestionId.add(parent1QuestionList[i].get(step).getQuestionId());
}
parent1QuestionList[i].remove(step);
}
}
//若满足条件则从父类2一中随机抽取一道不重复的题目添加
if (parent2QuestionList[i]!=null){
if (parent2QuestionList[i].size() > 0 && questionList[i].size()<targetSize){
int step = random.nextInt(parent2QuestionList[i].size());
if (!existQuestionId.contains(parent2QuestionList[i].get(step).getQuestionId())){
questionList[i].add(parent2QuestionList[i].get(step));
existQuestionId.add(parent2QuestionList[i].get(step).getQuestionId());
}
parent2QuestionList[i].remove(step);
}
}
if (parent1QuestionList[i].size()==0 && parent2QuestionList[i].size()==0 || questionList[i].size()>=targetSize || runningTimes > targetSize*2){
run = false;
}
// 避免死循环变量
runningTimes++;
}
}
child.setQuestionList(questionList);
return child;
} -
变异。交叉之后子代经历的变异,实际上是子代基因按小概率扰动产生的变化。依据个体编码表示方法的不同,可以有以下的算法:实值变异、二进制变异。我使用的是实值变异,在进化的过程中每道题都将有k的概率会变异,发生变异后将从题库中抽取一道具有rule相关限定条件的新题目作为变异因子代替原有基因片段。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29/**
* 基因突变
* @param paper
*/
public void mutate(ExaminationPaper paper) {
for (int i = 0; i < 5; i++) {
for (int j = 0; j < paper.getQuestionList()[i].size(); j++) {
if (Math.random() < mutationRate) {
TExaminationQuestion mutationQuestion = paper.getQuestionList()[i].get(j);
// 设置数据库查询条件构造器
QueryWrapper wrapper = new QueryWrapper();
wrapper.eq("difficulty",mutationQuestion.getDifficulty());
wrapper.eq("chapter",mutationQuestion.getChapter());
wrapper.eq("type",mutationQuestion.getType());
wrapper.eq("examination_course_id",mutationQuestion.getExaminationCourseId());
wrapper.eq("is_approved",mutationQuestion.isApproved());
wrapper.ne("question_id",mutationQuestion.getQuestionId());
// 查询同条件下id不同的题目
List<TExaminationQuestion> newQuestion = tExaminationQuestionDao.selectList(wrapper);
if (newQuestion.size() != 0){
//System.out.println("发生基因突变了======原题目突变为新题目");
Random random = new Random();
paper.setQuestion(i,j,newQuestion.get(random.nextInt(newQuestion.size())));
}
}
}
}
} -
进化。以种群为单位,逐步去执行进化算法使其适应环境,即适应度值更高。迭代过程中执行的进化算法就包括了选择、交叉、变异三个步骤。其中为了相对提高迭代收敛的速度,我弄了种群精英主义,即每一轮的进化过程中,保留该种群中最优秀的单一个体,即适应度最高的个体,添加至进化后的种群中,使种群的最优适应度始终>=进化前种群。
1 | /** |
